
For example, using the property log (mn) = log m + log n we can write We can use the properties of log in simplifying the logarithmic functions and expand/compress the logarithms. What are the Applications of Properties of Log? There are 4 important logarithmic properties: The logarithmic properties are used to compress/expand logarithms.

i.e., they are applicable for log, ln, (or) for logₐ. The logarithmic properties are applicable for a log with any base.Important Notes on Logarithmic Properties Here are the examples of both forms of the property: By multiplying it on both sides by log꜀ b, we get another form of change of base rule. Hence, the change of base property of log is derived. Substituting the values of x, y, and z here: Let us convert these equations into logarithmic form. Let log b a = x, log꜀ a = y, and log꜀ b = z. Let us derive the change of base rule now. If we apply the change of base property to log₅ 2, we get But what if we have to calculate a logarithm with some other base, say log₅ 2? This property is very helpful in calculating such logarithms.
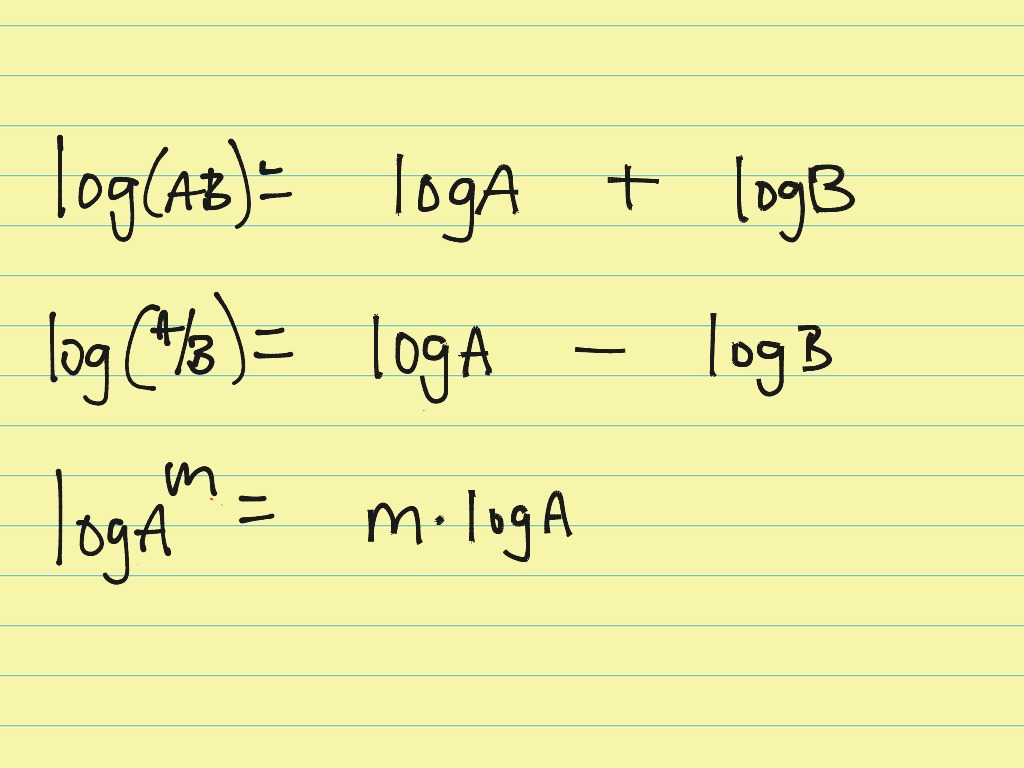
One is log (with base 10) and the other is ln (with base 'e'). We know that we have two buttons on the calculator to evaluate logarithms. It means that log b a can be written as the quotient of two logarithms (log a)/(log b) where both logs should be of the same base (say c). The change of base property says log b a = (log꜀ a) / (log꜀ b). We will study each property one by one in detail along with their derivations in the upcoming sections. (follows from the change of base rule and power property)Īll the properties of log are mentioned below.
answer.The properties of log are nothing but the rules of logarithms and these are derived from the exponent rules. Use a calculator and get all the parentheses and order of operations right. Now just approximate log8000 on a calculator Simplify since log10ˣ=x the left side is just x and it becomes x=log8000 Then after getting all the variable terms on one side and the constant terms on the other, factor out the variable.)Īlready isolated exponent term and it's not a base of 10ĭivide out the ln5 so it becomes x=ln134/ln5Īlready isolated exponent term and it is a base of 10 so take the common logs of both sides Isolate variable (you may need to distribute if you change logbˣ to xlogb. Simplify (lnbˣ=xlnb or lneˣ=x or log10ˣ=x)ģ. It actually doesn't matter if you take the common or natural log, it just helps with a shortcut later But you'll still get the same answers with either one.Ģ.

If the base is not 10 then take the natural log of both sides of the equation (not actually calculate it just write it down) P.S. If the base is 10 then take the common log of both sides of the equation (not actually calculate it just write it down). If the original inequality is ≤ or ≥ then include the ZERO boundary points in the answer, but not the boundary points from the denominator being undefinedġ. Put into form f(x) >/ 0 for all numbers, x, in the intervalī) If the value of f is negative then f(x) then don't include the boundary points in the answer.


 0 kommentar(er)
0 kommentar(er)
